Lesson 4 - Systems of Linear Equations - Solving by Graphing

NOTES

        1. This tutorial in Taglish is based on Module: Equations 2 prepared and published by the Department of Education of the Philippines for the Alternative Learning System (ALS) program.

        2. Sorry for any typographical and/or grammatical error that has been missed.

       3. Please comment for any incorrect answers.

=================================================

        

Matapos nating mapag-aralan ang mga araling nakapaloob sa ALS Module Equations 1, dadako naman tayo sa ALS Module Equations 2 upang pag-aralan din ang mga leksyon dito. Ang mga ito ay magbibigay sa iyo ng karagdagang kaalaman sa pangunahing konsepto ng balance o equality na kinakatawan mathematically ng mga equation. Ito ay magtuturo sa iyo ng higit pa tungkol sa mga konsepto ng mga equation at kung paano ito makakatulong sa iyong lutasin ang mga problemang nangyayari sa iyong pang-araw-araw na buhay.

        Sa pagpapatuloy ng ating pag-aaral hinggil sa equation, ang bahaging ito ay kinabibilangan ng tatlong aralin:

Lesson 4 — Systems of Linear Equations 

Lesson 5 — Applications of Linear Equations 

Lesson 6 — Quadratic Equations

Ano ang Matutunan Mo sa Modyul na Ito?

        Pagkatapos mong pag-aralan ang modyul na ito, dapat ay kaya mo nang:

• 1-solve ang mga sistema ng mga linear na equation;

• gumamit ng mga linear na equation sa paglutas ng mga word problems; at

• mahanap ang mga values ng x sa ibinigay na mga quadratic equation

Lesson 4 — Systems of Linear Equations 

MATUTO TAYO

        Sa nakaraang module, natutunan nain kung paano i-graph ang isang linear equation na may dalawang variable sa pamamagitan ng paggamit ng x-intercept at ng y-intercept o sa pamamagitan ng paggawa ng table of values. Sa araling ito, muli nating tatalakayin ang mga linear equation na may dalawang variable. Ngunit sa pagkakataong ito, lulutasin natin ang dalawang linear equation na may 2 unknowns hindi lamang sa pamamagitan ng graph kundi pati na rin sa paggamit ng Algebra.

        Ang systems ng equation na katulad ng set na ibinigay sa itaas ay tinatawag na simultaneous equations dahil ang dalawang equation ay kumakatawan sa dalawang kundisyon na ipinataw nang sabay sa mga variables. Ang mga values ng mga variables na nakakatugon sa parehong equations ay sinasabing mga solutions of system of equations. Sa graph, ang bawat solusyon ay tumutugma sa isang punto ng intersection ng mga graph ng dalawang equations.

Halimbawa 1

        Solve the following graphically then check.

x + y = 6

       -3x + y = 2

        Maaari naming i-graph ang isang linear equation sa pamamagitan ng paggawa ng isang talahanayan ng mga ordered pairs o sa pamamagitan ng paggamit ng x- at ang y-intercepts. Gamitin natin ang mga intercepts.

        Para sa x + y = 6

    Kapag x =0, 0 + y = 6

                      y = 6

        Samakatuwid ang (0,6) ay isang solution.

        Kapag ang y = 0, x + 0 = 6

               x = 6

Samakatuwid, ang (6, 0) ay isa ring solution.

Para sa -3x + y = 2

Kapag x =0, -3(0) + y = 2 

                                               0 + y = 2

             y = 2

Samakatuwid, ang (0, 2) ay isang solution.

Kapag y = 0,         -3x + 0 = 2 

                                              -3x = 0

        -3x/-3 = 2/-3

                 x = -2/3

Samakatuwid, ang (-2/3, 0) ay isa ring solution.

        Ito ang magiging graph ng dalawang equations kapag inilapat natin ang kanilang mga solutions sa coordinate plane.  

        Makikita sa graph na ang point  (1, 5) ay isa ring posibleng solution. I-check natin sa pamamagitan ng paghalili ng mga ito sa ating orihinal na equations.

Para sa x + y = 6  ==>1 + 5 ≟ 6 ==> 6 = 6

Para sa -3x + y = 2 ==> -3 + 6 ≟ 2 ==> 2 = 2

        Samakatuwid, ang solution para sa ibinigay na system of linear equations ay

                             (1, 5).

Halimbawa 2

        Solve this system by graphing:

-4x + 10y = 6

2x – 5y = 3

Para sa -4x + 10y = 6

Kapag x =0, -4(0) + 10y = 6

                                                      0 + 10y = 6 

                                                       10y/10 = 6/10 

                                                     y = 6/10 = 3/5

Samakatuwid, ang (0, 3/5) ay isang solution.

Kapag y = 0,         -4x + 10(0) = 6

                                             -4x + 0 = 6 

                                                             -4x = 6 

                                                         -4x/-4 = 6/-4 

                                                                 x = -3/2 o -1 ½

Samakatuwid, ang (-3/2, 0) ay isa ring solution.

         Para sa 2x – 5y = 3

Kapag x = 0,             2(0) – 5y = 3 

                                                0 – 5y = 3 

                                                         -5y/-5 = 3/-5 

                                                                 y = -3/5

Samakatuwid, ang (0, -3/5) ay isang solution.

Kapag y = 0,             2x – 5(0) = 3 

                                                         2x – 0 = 3 

                                                            2x/2 = 3/2 

                                                                 x = 3/2 o 1 ½.

Samakatuwid, ang ( 3/2, 0) ay isa ring solution.

        I-plot ang mga solutions ng dalawang equations sa coordinate plane

        Mapapansin na ang dalawang linya ay parallel. Wala silang magkaparehong point o hindi sila nag-intersect. Upang masuri kung sila nga ay parallel, i-solve kung pareho ang kanilang mga slopes

        Para sa -4x + 10y = 6 (Gawin ito sa pormang y = mx + b)

                    10y = 4x + 6

               10y/10 = 4x/10 + 6/10

                        y = 2/5x + 3/5

        Samakatuwid, ang slope ay 2/5 at ang y-intercept ay 3/5.

        Para sa 2x - 5y = 3

                            -5y = -2x + 3

                       -5y/-5 = -2x/-5 + (3/-5)    

                              y = 2/5x - 3/5

Samakatuwid, ang slope ay 2/5 at ang y-intercept ay -3/5.

        Dahil magkapareho ang slope ng dalawang equations, masasabing no solution ang system. Ang solution set ay {} o null set.

Halimbawa 3

        Solve the following by graphing:

y = -2x + 1

2x + y = 1

Para sa y = -2x + 1

                    Kapag ang x = 0, y = 2(0) + 1 

                                                        y = 0 + 1

                y = 1

Samakatuwid, ang (0,1) ay isang solution.

Kapag ang y = 0,         0 = -2x + 1 

                                                    -2x = -1

        -2x/-2 = -1/-2 

                                                       x = 1/2 

Samakatuwid, ang (1/2, 0) ay isa ring solution.

                Para sa 2x + y = 1

                    Kapag ang x = 0, 2(0) + y = 1 

                                                            0 + y = 1

                          y = 1

Samakatuwid, ang (0,1) ay isang solution.

Kapag ang y = 0,         2x + 0 = 1 

                                                              2x = 1

                   2x/2 = 1/2 

                                                                x = 1/2 

Samakatuwid, ang (1/2, 0) ay isa ring solution.

    Mapupuna na ang dalawang equations ay may magkaparehong solution sets. 

            Kapag nai-plot natin ang solution sets ng dalawang equations, ito ang kalalabasan ng kanilang graph: 

            Mapapansin na ang mga graphs ng dalawang equations ay magkapareho o ang mga ito ay nag-coincide o nagkalapat. Ang mga solutions ng sistema ay ang mga ordered pairs na (0, 1) at (1/2, 0) sa alinmang equation.

            Mapapatunayan nating magkapareho nga ang graph ng dalawang equation o ang mga ito ay nagkalapat kung ang kanilang mga slopes at y-intercept ay magkapareho. Tingnan natin.

            Para sa y = -2x + 1,  dahil ang equation ay nasa slope-intercept na, ang slope nito ay -2 at ang y-intercept ay 1.

            Para sa 2x + y = 1, gawin muna natin ito sa slope-intercept form:   

2x + y = 1 ==> 2x – 2x + y = -2x + 1 ==> y = -2x + 1. Ang slope ay -2 at ang y-intercept ay 1. 

            Dahil ang dalawang equations ay may magkaparehong slope at y-intercept, sila ay tinatawag na equivalent equations.

    Ang kanilang solution set ay isang infinite o walang katapusang set na maaaring isulat ng ganito:

     {( x,y) |  2x + y =  1}

            at basahin bilang “the solution set is the set of all ordered pairs (x, y) such that 2x + y = 1”.

Summary

To solve a system of linear equations in two variables graphically, first, graph the equations on the same coordinate plane. Then consider the following:

1. If the graphs are parallel, the system has no solution.

2. If the graphs coincide, the system has an infinite set of solutions.

3. If the graphs intersect, the coordinates of the point of intersection form the solution of the system.

Pagsasanay

1. Determine whether the given ordered pair is a solution to the system of linear equations or not.

(3,2) 2x + 3y = 12

        x – 4y = -5

2. Determine whether the given ordered pair is a solution to the system of linear equations or not.

(2, 5) y = -x + 7

        2x = y – 1

3. Graphically, find the solution set of the system: 

                        x - 2y = 1

                        x -   y = 2 

4. Graphically, find the solution set of the system: 

                        y = 2x + 4

                        2x -  y = 2 

 5. Find the solution set of the system:

                          x = y

                        x + y = 3 by graphing. Use fractions if necessary.

6. Solve this system of equations graphically and check your solution:

                        x = y + 1

                                2x + y = -7

ANSWERS:

Request for copy of your ALS COR , Certificate or Diploma

Nawawala ba o naiwala ang iyong COR, Diploma at/o ALS Certificate?

Para po sa nanghihingi ng certified copy, photocopy, or original ng inyong Certificate of Rating (COR), Diploma o ALS Certficate, at anumang katanungan hinggil sa programa ng Alternative Learning System at/o Philippine Educational Placement Test (PEPT), makipag-ugnayan po lamang sa ibaba:

Bureau of Education Assessment (BEA)

Office Address: 2/F, Bonifacio Bldg., DepEd Complex, Meralco Ave., Pasig City

Tel. Nos.: (02) 631-2571 / 631-2588 / 631-2589 / 631-2591 / 687-6717 / 631-6921

Office Hours: Monday to Friday, 8:00am-5:00pm (except weekends, holidays, and work suspensions)

Maaari rin po kayong mag-email sa  Bureau of Education Assessment (BEA), sa  bea.ead@deped.gov.ph at/o bea.od@deped.gov.ph.

Dahil po sa daming kahilingan at katanungan sa BEA, mangyari pong maghintay ng kaukulang panahon. Sundin po ang sinasaad ng iyong email o ang sinagot sa iyong pagtawag sa telepono. 

Answers to Exercises: Lesson 3 - Linear Equations In Two Variables

Narito ang mga sagot sa Pagsasanay ng Lesson 3 - Linear Equations In Two Variables | ALS Module Functions 1

Mga Sagot sa Pagsasanay

1. Determine whether (2, -1) is a solution of  y - 4 = 5(x – 3).

Ihalili lamang ang binigay na mga values sa equation at tingnan kung ang kaliwang panig ay katumbas o kapareho ang value ng kanang panig.

(2, -1) ==>  (x, y)

  y – 4 = 5(x – 3)

-1 – 4 ≟ 5(2 – 3)

      -5 ≟ 5(-1)

      -5 = -5 

     Samakatuwid, ang (2,-1) ay solution ng  y – 4 = 5(x – 3).

2. What are the coordinates of the point where the graph of the equation 

    2x + 3y = 3 crosses the y-axis?

Dahil nag-cross ang graph ng 2x + 3y = 3 sa y-axis, ibig sabihin, ang value ng x ay zero sa ordered pair na ito.

Kung gayon, kung x = 0, ang y ay:

2x + 3y     = 3

 2(0) + 3y = 3

            3y = 3

         3y/3 = 3/3

              y = 1

Samakatuwid, ang coordinates ng point kung saan tumawid ang equation 

2x + 3y = 3 ay (0, 1).

3. What are the coordinates of the point where the graph of the equation 

        y = -3x – 4 crosses the x-axis?

Dahil tumawid ang graph ng equation y = -3x – 4 sa x-axis, ibig sabihin ang value ng y sa coordinate na ito ay zero (0). Kung gayon, kung y = 0, ang value ng 

x ay:

    y = -3x – 4

    0 = -3x – 4

  3x = -4

       3x/3 = -4/3

    x = -4/3 or -1 1/3

Samakatuwid, ang coordinates ng point kung saan tumawid sa x-axis ang equation y = -3x – 4  ay (-4/3, 0) o (-1 1/3, 0).

4. Find the intercepts of the equation 3y = 5x, then draw its graph.

Upang mahanap ang x-intercept, ihalili ang zero (0) sa value ng y sa equation upang mahanap ang x.

3y     = 5x

3(0)  = 5x

    5x = 0

 5x/5 = 0/5

      x = 0

Upang mahanap ang y-intercept, ihalili ang zero (0) sa value ng x sa equation upang mahanap ang y.

3y = 5x

 3y= 5(0)

 3y = 0

      3y/3 = 0

   y = 0

Dahil parehong nasa origin ang ating x-intercept at y-intercept, hahanap pa tayo ng points upang ma-graph natin ang equation.

Maglalagay tayo ng arbirtrary o pansamantalang value ng x upang mahanap ang y.

Kung x = 3, ang y ay:

3y = 5x

3y = 5(3)

3y = 15

     3y/3 = 15/3

  y = 5

Ang ating dalawang points ay (0, 0) at (3, 5).

Maaari na nating i-drowing ang ating graph.

5. Write in slope-intercept form if the slope is ¾ and the y-intercept is – ½.

The slope-intercept form is y = mx + b, where m is the slope and b is the 

    y-intercept.

Dahil ang m = ¾ at ang y-intercept = -1/2, samakatuwid ang ating equation na nasa slope-intercept form ay:

        y = ¾ x – ½ 

Please follow this blog for more ALS tutorials, reviewers, and information.

Kindly subscribe to my Youtube channel:

        Solid Ka-ALS

Lesson 3 - Linear Equations in Two Variables | ALS Module - Equations 1

Lesson 3 – Linear Equations In Two Variables

        Sa nakaraang aralin ay nalaman natin ang mga konsepto at terminong karaniwang ginagamit sa Algebra. Natuto tayong mag-solve ng linear equation na may iisang variable o unknown.

Sa araling ito ay pagtutuunan naman natin ang pagresolba ng linear equations na may dalawang variables o unknowns.

MATUTO TAYO

        Ang isang equation tulad ng 4x + 5 = 21 ay may isang value, 4, bilang solusyon nito. Ang isang equation na may dalawang variable tulad ng y = 2x + 1 ay may maraming solusyon na maaari nating isulat bilang ordered pairs ng mga numero.

         Para sa isang equation tulad ng y = 2x + 1, isinusulat natin ang ordered pairs sa ganitong anyo,   (x, y).

Halimbawa 1

Determine whether (3, 7) is a solution of y = 3x - 2. (Tukuyin kung ang (3,7) ay isang solusyon ng y = 3x – 2)

Para gawin ito, ihalili lamang ang ordered pair (x, y) ==> (3,7) sa equation, tulad nito:

y = 3x – 2

7 ≟ 3(3) – 2

7 ≟ 9 – 2

7 = 7 

Samakatuwid, ang equation ay tama. Ang ordered pair na (3,7) ay isang solution ng y = 3x -2.

        We can find solutions to equations in two variables by choosing a value for one variable, substituting it, and computing the equation to find the value of the other variable. (Maaari tayong makahanap ng mga solusyon sa mga equation na may dalawang variables/unknowns sa pamamagitan ng pagpili o paglapat ng isang value sa isang variable, ihalili ito at i-compute ang equation upang mahanap ang value ng ikalawang variable/unknown.)

Halimbawa 2

Find 3 solutions for the equation 3x + y = 9.

        Mas madaling masasagot ang problema kung kukunin muna natin ang value ng y. Gamit ang transposition, ang ating equation na 3x + y = 9 ay magiging ==>

y = -3x + 9

        Ngayon, maaari na tayong maghalili ng value ng x upang makuha ang value ng y.

Kung ang value ng x ay zero (0), ang value ng y ay:

          y = -3(0) + 9

          y = -3 + 9 

          y = 6

Kung gayon, ang ordered pair na (0,6) ay isang solution ng equation.

Kapag pinili natin ang 2 bilang value ng x, ang value ng y ay magiging:

y = -3(2) + 9 

                y = -6 + 9 

                y = 3

Ang ikalawang solution ng ating equation ay ang ordered pair na (2,3).

Ngayon, ihalili naman natin ang –1 bilang x.

     y = -3(-1) + 9 

             y = 3 + 9 

             y = 12

Ang ating ikatlong solution ay (-1, 12).

        P’wede nating itala sa isang table/talahanayan ang mga ordered pairs upang madaling makita ang ilang solutions sa ating equation na 3x + y = 9. 

        Alam na natin ngayon na ang solution ng isang  linear equation na may 2 variables ay isang ordered pair ng mga numero. Ang mga ordered pairs na ito ay maaaring i-graph sa isang coordinate plane. Ang graph ng isang equation ay isang  drowing na kumakatawan sa mga solutions nito.  

Halimbawa 3

Graph the equation 4x = 8 – 2y.

        Bago nating mai-graph ang equation, hanapin muna natin ang mga solutions o ordered pairs nito.

Step 1 Gawing simple ang equation (ayon sa natutunan natin sa lesson 2).

4x = 8 – 2y 

2y = - 4x + 8  

2y/2 = -4x/2 + 8/2

y = -2x + 4

Step 2 Maghalili ng value ng x para makuha ang value ng y.

y = -2x + 4

Kung ang x = 0, y = -2(0) + 4 =  0 + 4 = 4

        x = -1 y = -2(-1) + 4 =  2 + 4 = 6

        x = -2 y = -2(-2) + 4 = 4 + 4 = 8

        x = 2 y = -2(2) + 4 = -4 + 4 = 0

        x = 4 y = -2(4) + 4 = -8 + 4 = -4

Step 3 Ilagay sa table o talahanayan ang mga values.

Step 4 I-plot ang mga points na (0, 4), (-1, 6), (-2, 8), (2, 0), at (4, -4) sa                                 coordinate plane. 

        Mapapansin sa graph na ang lahat ng points o ordered pairs ay nakalapat sa isang straight line. Kung magpa-plot pa tayo ng iba pang solutions, ang mga ito ay lalapat din sa nasabing tuwid na linya. Ang linya ay ang graph ng ating equation na 4x = 8 – 2y. Ang lahat ng points sa linya ay solusyon sa equation na ito.

Matuto Tayo

        Sa pag-graph ng mga linear na equation, maaaring tumawid ang isang tuwid na linya sa x-axis sa ilang points at maaari ring tumawid sa y-axis sa iba pang mga points. Ang mga points na ito ay tinatawag na mga intercept ng isang graph.

Ang x-intercept ay ang x-coordinate (value ng x) ng point kung saan tumatawid ang isang graph sa x-axis. Ang y- intercept, sa kabilang banda, ay ang y-coordinate (value ng y) ng point kung saan ang isang graph ay tumatawid sa y-axis.

        Ang bawat point sa x-axis ay may y-coordinate na zero at ang bawat point sa 

y-axis ay may x-coordinate na zero. Kapag pinagsama ang mga obserbasyon na ito kasama ang ideya ng mga intercept, maaari nating ibuod ang mga sumusunod:

        1.  Ang x-intercept ng isang graph ay ang x-coordinate ng punto na may y-coordinate na zero (0).

2.  Ang y-intercept ng isang graph ay ang y-coordinate ng punto na may x-coordinate na zero (0).

        Sa madaling salita, upang mahanap ang x-intercept ng graph ng isang equation, dapat nating hayaan ang y = 0 sa equation. 

Upang mahanap ang y-intercept, dapat nating hayaan ang x = 0 sa equation. 

Kapag naghahanap ng mga intercept, hindi kinakailangang ihiwalay ang alinmang variable.

Halimbawa 4

Find the x-intercept and the y-intercept of the line for the equation 2x + y = 1.

Kapag ang x = 0, ang y ay:

2(0) + y = 1 

                    0 + y = 1 

                          y = 1

Samakatuwid, ang y-intercept ay 1.

Kapag ang y = 0, ang x ay:

2x + 0 = 1 

                      2x = 1 

                        x = ½

Samakatuwid ang x-intercept ay ½.

        Ang graph ng mga puntos na (0, 1) at (1/2, 0) ay makikita sa ibaba:      

Halimbawa 5

Graph the equation  x – y = 0.

Step 1 Hanapin ang x at y-intercept ng equation.

Kapag ang x = 0, ang y ay:

0 – y = 0 

                              y = 0

Samakatuwid, ang y-intercept ay 0.

Kapag ang y = 0, ang x ay:

x – 0 = 0 

                              x = 0

Samakatuwid, ang x-intercept ay 0 rin.

        Anong nangyari? Mukhang magkakaproblema tayo dito dahil ang x-intercept at y-intercept ay parehong zero (0) o nasa origin. Kapag nangyari ito, kailangan nating maghanap ng isa pang point sa graph sa pamamagitan ng pagpili ng arbitrary o pansamanalang  x-value at hanapin ang katumbas na y-value nito.

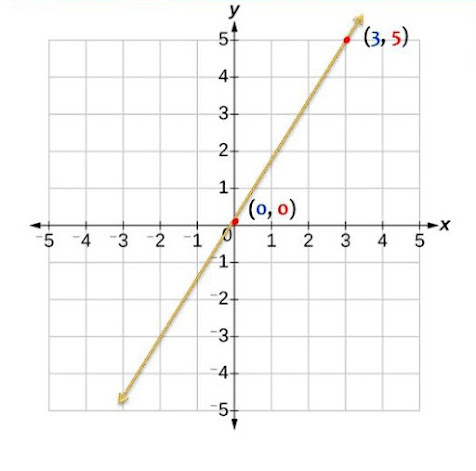
Ang una nating solution o point ay (0,0). Humanap pa tayo ng isa pang point.

Sa ating equation na x – y = 0, kung x = 2, ang y ay magiging: 

                    2 – y = 0 

                         -y = -2 

                          y = 2.

        Ang ating ikalawang puntos ay (2,2).

        Ang graph ng mga puntos na (0, 0) at (2, 2) ay makikita sa ibaba:      

Summary

• A solution of an equation with two variables is an ordered pair of numbers that can be plotted on a coordinate plane.

• A graph of an equation is a drawing that represents its solutions.

• The intercepts of a graph are the points where a straight line crosses the x- and y-axes.

• The x-intercept is the x-coordinate of the point at which a graph crosses the x-axis.

• The y-intercept is the y-coordinate of the point at which a graph crosses the y-axis.

• In the formula, y = mx + b, m is the slope of the line while b is the coefficient of y.

• To graph a linear equation of the form ax + by = c using the intercept method, we follow these steps:

        1. Find the x-intercept by letting y = 0 in the original equation.

        2. Find the y-intercept by letting x = 0 in the original equation.

        3. Write the ordered pair corresponding to each intercept.

        4. Plot the intercept points and connect them with a straight line.

• The equations for most lines may be given by the slope-intercept form 

                y = mx + b.

        Note that m is the slope of the line. The arbitrary constant, b, is the y-intercept.

        Without drawing a graph of the equation, determine the slope and y-intercept of the equation y = 2x + 5.

The coefficient of x is 2 and the constant term is 5. Thus m = 2 and b = 5.

Pagsasanay

1.    Determine whether (2, -1) is a solution of y - 4 = 5(x – 3).

2.   What are the coordinates of the point where the graph of the equation 

        2x + 3y = 3 crosses the y-axis?

3.   What are the coordinates of the point where the graph of the equation 

        y = -3x – 4 crosses the x-axis?

4.   Find the intercepts of the equation 3y = 5x, then draw its graph.

5.   Write in slope-intercept form if the slope is ¾ and the y-intercept is – ½.

For the answers, please CLICK this link: ANSWERS to Exercises: Lesson 3 - Linear Equations In Two Variables

Reference: ALS Module - Equations 1

Lesson 2 - Linear Equations in One Variable: ALS Module - Equations 1

 Lesson 2 – Linear Equations in One Variable

(Image from https://www.cmuse.org)

Simulan natin ang pag-aaral sa pamamagitan ng pag-alam sa mga konsepto ng mga sumusunod na termino:

1. Ang equality ay isang mathematical na pahayag kung saan ang dalawang expression ay pantay o may parehong value/halaga.

Kung gayon, ang 3x = 15 at 2y + 4y = 6y ay mga equation.

2. May dalawang uri ng equalities. Ang mga ito ay ang equations at identities.

3. Ang identity ay isang equality kung saan sa mga variable ay maaaring magkaroon ng anumang value at kung saan ang equality ay magiging tama sa lahat ng pagkakataon. Nangangahulugan ito na ang kaliwang bahagi ng isang equation ay palaging katumbas ng kanang bahagi kahit anong value/halaga ang ipinalit para sa variable.

Halimbawa, isaalang-alang natin ang ating equality sa itaas na:

2y + 4y = 6y

Kung ang value ng ating variable y ay 0 (zero), ang equation ay magiging ==>

2(0) + 4(0) = 6(0)

0 + 0 = 0

0 = 0

Kung ang y naman ay may value na 1, ang equation ay magiging ==>

2(1) + 4(1) = 6(1)

2 + 4 = 6

6 = 6

Mapapansin natin sa itaas na kahit ano ang value na ipalit natin sa ating variable, ang equation ay magiging tama o totoo.

4. Dahil walang mga paghihigpit o restrictions sa mga value na  maaaring mayroon ang y, ang 2y + 4y = 6y ay isang halimbawa ng unconditional equality.

5. Sa kabilang banda, ang isang equation ay isang conditional equality kung ang variable/s nito ay may partikular o iisang value lamang.

6. Ang solution o root ng isang equation ay anumang numero na, kapag pinalitan ang variable, ay gagawing pantay ang dalawang panig ng isang equation. Masasabi na ang root ang siyang nagbigay tama sa isang equation.

Halimbawa, sa equation na 5x – 13 = -3x + 19

Kung 4 ang ipapalit natin sa x sa equation, ito ay magiging ==>

5(4) – 13 = -3(4) + 19

   20 – 13 = -12 + 19

     7 = 7

Samakatuwid, ang 7 ay solution o root ng equation.

Samantala, kung 2 ang ipapalit natin sa x sa equation, ito ay magiging ==>

5(2) – 13 = -3(2) + 19

   10 – 13 = -6 + 19

   -3 ≠ 13

Dahil ang -3 ay hindi katumbas ng 13, masasabi natin na ang 2 ay hindi isang solution o root ng equation.

7. Ang set ng lahat ng mga solution ng isang equation  ay tinatawag na solution set. Upang malutas ang isang equation, nangangahulugang dapat nating  hanapin ang solution set nito.

8. Ang linear equation ay isang equation na ang lahat ng  term ay nasa first degree. Nangangahulugan ito na ang pinakamataas na exponent o kabuuan ng mga exponent ng alinman sa mga termino ng isang equation ay 1.

    Ang graph ng isang linear equation ay straight line. 

9. Ang linear equations ay maaaring uriin sa linear equations in one variable, linear equations in two variables, linear equations in three variables at iba pa.

10.   Ang linear equations in a variable, x, ay maaaring isulat sa pormang   

        ax + b = 0 kung saan ang a ay hindi maaaring zero (0).

11.   Ang equivalent equations ay algebraic equations na may magkaparehong solution sets o roots.  Ang pag-add o pag-subtract ng parehong numero o expression sa pagkabilang panig ng equation ay magreresulta ng equivalent equations.

Halimbawa, sa equation na x – 2 = 8, ang ating makukuhang sagot ay:

x -  2 = 8 

                      x = 8 + 2

      x = 10

Sa parehong equation na x – 2 = 10, 

kapag nagdagdag tayo ng 5 sa kaliwa at sa kanang panig ng equation, hindi pa rin magbabago ang equation. Subukin natin.

x – 2 + 5 = 8 + 5

      x + 3 = 13

            x = 10

Samakatuwid, ang x – 2 = 8 at x – 2 + 5 = 8 + 5 ay equivalent equations.

Tandaan lamang na kung ano ang ginawa sa kaliwang panig (left side) ay ganoon din ang gagawin sa kanang panig (right side) ng equation.

Hindi lamang addition at subtraction ang maaaring gawin sa magkabilang panig ng equation. Maaari ring gawin ang multiplication at division subalit ang numerong gagamitin ay dapat ay non-zero.

12.    Ang proseso ng paglipat ng isang termino sa kabilang panig at pagbabago ng sign nito ay tinatawag na transposition.

Halimbawa:

- 4m    =   - 5m – 3

-4m + 5m   =   - 5m – 3 + 5m

       m = 0 – 3

               m = -3

Sa pagso-solve ng linear equation in one variable, pagsamahin o ilipat natin ang variable sa kaliwang panig ng equation at ang constant naman ay nasa kanang panig.

13.    Ang literal equation ay isang equation kung saan ang ilan sa mga constant ay hindi tinukoy ngunit kinakatawan ng mga titik tulad ng a, b, c o d. Ang mga titik na ito ay tinatawag na  literal constants o arbitrary constants.

Samakatuwid,  ang 5x = Q ay isang halimbawa ng literal equation kung saan ang x ay isang variable at ang Q naman ay isang literal or arbitrary constant. 

Narito ang ilan pang halimbawa ng literal equations:

A = πr2         (area of a circle)

P = 2L + 2W         (perimeter of a rectangle)

C=5/9  (F −32)       (Fahrenheit to Centigrade)

P = 4s         (perimeter of square)

Mapapansin na ang mga equations sa itaas ay mga formulas. Ito ay dahil ang lahat ng formulas ay literal equations.

How to Solve Linear Equations in One Variable

Matapos nating mapag-aralan ang konsepto ng iba’t ibang termino, handa na tayong mag-solve ng linear equation na may isang variable. Paano natin ito gagawin?

Example A: Solve 5x – 7 + 4x = 2x – 28 + 4x.

Step 1 Gawing simple ang equation sa pamamagitan ng pagsasama-sama ng magkaparehong terms.

5x – 7 + 4x = 2x – 28 + 4x ==>

        9x – 7 = 6x - 28

Step 2 Ihiwalay ang variable at ilagay ito sa kaliwang panig at ang constant naman ay ilagay sa kanang bahagi gamit ang addition property of equality o sa pamamagitan ng transposition.

         9x – 7 = 6x – 28

  9x – 7 + 7 = 6x – 28 + 7

      9x = 6x – 21

      9x – 6x = 6x – 6x – 21

      3x = -21

Step 3 Gamitin ang multiplication property of equality o i-divide ang dalawang panig ng  numerical coefficient ng variable

Step 3 Ihalili ang nakuhang value ng variable sa orihinal na equation upang matiyak na tama ang nakuhang solution, root, o sagot.

                                              x = - 7

                          5x – 7 + 4x = 2x – 28 + 4x 

                      5(-7) – 7 + 4(-7) = 2(-7) – 28 + 4(-7)

                     -35 – 7 – 28 = -14 – 28 -28

                           -70 = - 70

Samakatuwid, x = - 7 ay ang solution o root ng  5x – 7 + 4x = 2x – 28 + 4x dahil natugunan nito ang equation.

Example B: Solve 3(x –2) + 6 = 5x + 2.

Step 1 Gamitin ang multiplication property over addition upang maalis ang mga  parentheses.

3(x –2) + 6 = 5x + 2 ==>

       3x – 3(2) + 6 = 5x + 2

    3x – 6 + 6 = 5x + 2

          3x + 0 = 5x + 2

                3x = 5x + 2

Step 2 Ihiwalay ang variable at ilagay ito sa kaliwang panig at ang constant naman ay ilagay sa kanang bahagi gamit ang addition property of equality o sa pamamagitan ng transposition.

   3x = 5x + 2

   3x – 5x = 5x – 5x + 2

          -2x = 2

Step 3 I-multiply ang magkabilang panig ng  multiplicative inverse ng –2, iyan ay −1/2.

-2x = 2

    −1/2 (−2𝑥) = −1/2 (2)

   x = -1

Step 4 Ihalili ang nakuhang value ng variable sa orihinal na equation upang matiyak na tama ang nakuhang solution, root, o sagot.

       x = - 1

                    3(x –2) + 6 = 5x + 2

          3(-1 – 2) + 6 = 5(-1) + 2

        3(-3) + 6 = - 5 + 2

            - 9 + 6 = -3

                   -3 = - 3

Samakatuwid, x = - 1 ay ang solution o root ng  3(x –2) + 6 = 5x + 2  dahil natugunan nito ang equation.

Example C: Solve 5(y + 3) - 4 = 5y - 8.

Step 1 Gamitin ang multiplication property over addition o distributive property upang maalis ang mga  parentheses.

       5(y + 3) - 4 = 5y - 8 ==>

 5(y) + 5(3) – 4 = 5y – 8

       5y + 15 – 4 = 5y – 8

Step 2 Gawing simple ang equation sa pamamagitan ng pagsasama-sama ng magkaparehong terms.

5y + 15 – 4 = 5y – 8

      5y + 11 = 5y - 8

Step 3 Ihiwalay ang variable at ilagay ito sa kaliwang panig at ang constant naman ay ilagay sa kanang bahagi gamit ang addition property of equality o sa pamamagitan ng transposition.

  5y + 11 = 5y - 8

  5y – 5y + 11 = 5y – 5y – 8

          11 = 8 ?

Samakatuwid, dahil ang 11 ay hindi maaaring equal sa 8, ang equation na  

 5(y + 3) - 4 = 5y - 8 ay no solution  (walang solution).

Matuto Tayo

Upang malutas ang mga equation na kinasasangkutan ng mga fraction na walang mga variable sa denominator, maaari tayong magsimula sa pamamagitan ng paggamit ng multiplication property of equality upang mawala ang mga fractions sa equation. Maaari nating gamitin ang anumang common multiple tulad ng least common multiple (LCM) ng lahat ng denominator sa equation. (Ang LCM ng 2 o higit pang bilang ay ang pinakamaliit na numero na multiple o factor ng mga bilang na ito). Ang LCM ay tatawagin na natin ngayong least common denominator (LCD).

Upang matutunan ito, unawain natin ang mga sumusunod na halimbawa.

Example 1

Step 1 I-multiply ang magkabilang panig ng LCD, 8, upang mawala ang mga fractions sa equation.

Step 2 Ihiwalay ang variable at ilagay ito sa kaliwang panig at ang constant naman ay ilagay sa kanang bahagi gamit ang addition property of equality o sa pamamagitan ng transposition.

6x + 16 = 3x – 32

6x – 3x + 16 – 16 = 3x  – 3x – 32 – 16

  3x + 0 = 0 - 48

        3x = - 48

Step 3 I-multiply ang magkabilang panig ng  multiplicative inverse ng 3, iyan ay 1/3.

       3x  =  - 48

         1/3(3𝑥  = −48)

             3𝑥/3 = −48/3

          x = - 16

Step 4 Ihalili ang nakuhang value ng variable sa orihinal na equation upang matiyak na tama ang nakuhang solution, root, o sagot.

       

                     

Samakatuwid, x = - 16 ay ang solution o root ng 3/4 𝑥 + 2 = 3/8𝑥 −4  dahil natugunan nito ang equation.

Example 2

        

Step 1 I-multiply ang magkabilang panig ng LCD, 3x, upang mawala ang mga fractions sa equation.

             

Step 2 Ihiwalay ang variable at ilagay ito sa kaliwang panig at ang constant naman ay ilagay sa kanang bahagi gamit ang addition property of equality o sa pamamagitan ng transposition.

2x - 6 = 12

  2x - 6 + 6 = 12 + 6

      2x = 18

Step 3 I-multiply ang magkabilang panig ng  multiplicative inverse ng 2, iyan ay 1/2.

2x = 18

 1/2(2𝑥 = 18)

    2𝑥/2 = 18/2

 x = 9

Step 4 Ihalili ang nakuhang value ng variable sa orihinal na equation upang matiyak na tama ang nakuhang solution, root, o sagot.

                x = 9

          2/3  − 2/𝑥  =  4/𝑥  

           2/3  − 2/9 = 4/9   

 

Step 5 I-multiply ang magkabilang panig ng LCD, 9, upang mawala ang fractions.  

 

                    9(2/3 − 2/9 = 4/9)

                    18/3 −18/9 = 36/9

     6 – 2 = 4

           4 = 4

                     

Samakatuwid, x = 9 ay ang solution o root ng  2/3  −2/𝑥=4/𝑥   dahil natugunan nito ang equation.  

Example 3

          

Step 1 Ihiwalay ang constant sa kaliwang panig  at ilagay ito sa kanang bahagi gamit ang addition property of equality o sa pamamagitan ng transposition.

Step 2 Gamitin ang cross multiplication. I-multiply ang numerator ng kanang panig sa denominator ng kaliwang panig at numerator ng kaliwang panig sa denominator ng kanang panig.

Step 3 Ilipat sa kanang panig ang constant sa kaliwang panig sa pamamagitan ng transposition.

2y + 5 = 9

2y + 5 – 5 = 9 – 5

2y = 4

Step 4 I-multiply ang magkabilang panig ng  multiplicative inverse ng 2, iyan ay 1/2.

        2y  = 4

1/2(2𝑦)  = 1/2(4)

      2𝑦/2 = 4/2  

           y = 2

Step 5 Ihalili ang nakuhang value ng variable sa orihinal na equation upang matiyak na tama ang nakuhang solution, root, o sagot. 

                

               Samakatuwid, y = 2 ay ang solution o root ng   3/(2𝑦+5 )+2/3=1   dahil natugunan nito ang equation.

Summary

• A solution or root of an equation is any number that, when substituted for the variable, makes both sides of the equation equal.

• The set of all solutions is called the solution set.

• We say that two equations are equivalent if they both have the same solution set—any solution of one is also a solution of the other.

• A linear equation is an equation of the first degree in any number of variables.

• Linear equations in a variable, x, can be written in the form ax + b = 0 where a ≠ 0.

• The process of moving a term to the other side of an equation and changing its sign is called transposition.

• A literal equation is an equation in which some of the constants are not specified but are represented by letters such as a, b, c or d.

• Formulas are literal equations.

ANSWERS: