Narito ang mga sagot sa Pagsasanay ng Lesson 3 - Linear Equations In Two Variables | ALS Module Functions 1
Mga Sagot sa Pagsasanay
1. Determine whether (2, -1) is a solution of y - 4 = 5(x – 3).
Ihalili lamang ang binigay na mga values sa equation at tingnan kung ang kaliwang panig ay katumbas o kapareho ang value ng kanang panig.
(2, -1) ==> (x, y)
y – 4 = 5(x – 3)
-1 – 4 ≟ 5(2 – 3)
-5 ≟ 5(-1)
-5 = -5
Samakatuwid, ang (2,-1) ay solution ng y – 4 = 5(x – 3).
2. What are the coordinates of the point where the graph of the equation
2x + 3y = 3 crosses the y-axis?
Dahil nag-cross ang graph ng 2x + 3y = 3 sa y-axis, ibig sabihin, ang value ng x ay zero sa ordered pair na ito.
Kung gayon, kung x = 0, ang y ay:
2x + 3y = 3
2(0) + 3y = 3
3y = 3
3y/3 = 3/3
y = 1
Samakatuwid, ang coordinates ng point kung saan tumawid ang equation
2x + 3y = 3 ay (0, 1).
3. What are the coordinates of the point where the graph of the equation
y = -3x – 4 crosses the x-axis?
Dahil tumawid ang graph ng equation y = -3x – 4 sa x-axis, ibig sabihin ang value ng y sa coordinate na ito ay zero (0). Kung gayon, kung y = 0, ang value ng
x ay:
y = -3x – 4
0 = -3x – 4
3x = -4
3x/3 = -4/3
x = -4/3 or -1 1/3
Samakatuwid, ang coordinates ng point kung saan tumawid sa x-axis ang equation y = -3x – 4 ay (-4/3, 0) o (-1 1/3, 0).
4. Find the intercepts of the equation 3y = 5x, then draw its graph.
Upang mahanap ang x-intercept, ihalili ang zero (0) sa value ng y sa equation upang mahanap ang x.
3y = 5x
3(0) = 5x
5x = 0
5x/5 = 0/5
x = 0
Upang mahanap ang y-intercept, ihalili ang zero (0) sa value ng x sa equation upang mahanap ang y.
3y = 5x
3y= 5(0)
3y = 0
3y/3 = 0
y = 0
Dahil parehong nasa origin ang ating x-intercept at y-intercept, hahanap pa tayo ng points upang ma-graph natin ang equation.
Maglalagay tayo ng arbirtrary o pansamantalang value ng x upang mahanap ang y.
Kung x = 3, ang y ay:
3y = 5x
3y = 5(3)
3y = 15
3y/3 = 15/3
y = 5
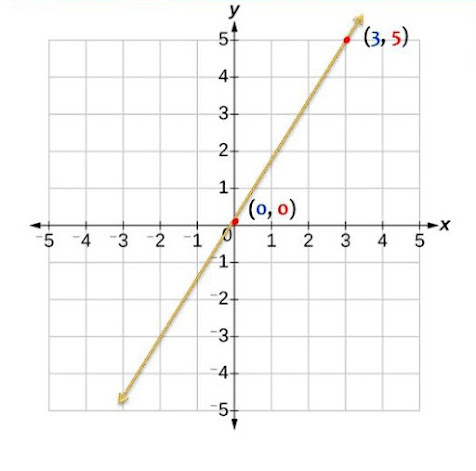
Ang ating dalawang points ay (0, 0) at (3, 5).
Maaari na nating i-drowing ang ating graph.
5. Write in slope-intercept form if the slope is ¾ and the y-intercept is – ½.
The slope-intercept form is y = mx + b, where m is the slope and b is the
y-intercept.
Dahil ang m = ¾ at ang y-intercept = -1/2, samakatuwid ang ating equation na nasa slope-intercept form ay:
y = ¾ x – ½
Please follow this blog for more ALS tutorials, reviewers, and information.
Kindly subscribe to my Youtube channel:


No comments:
Post a Comment